フレームワーク※で使われることが多い「レーダーチャート」「バブルチャート」「ボリュームチャート」は、複数のデータを視覚的かつ直感的に比較するのに適しています。すべてのチャートの原型となるマトリックスを作ってから、これら3つのチャートの形にしてみましょう。いずれも基本的なチャートですから、一般的な表計算ソフトで作成可能です。
※フレームワーク・・・経営戦略や業務改善など、さまざまなビジネス局面において、課題解決や現状分析をするための思考方法。思考の枠組み。
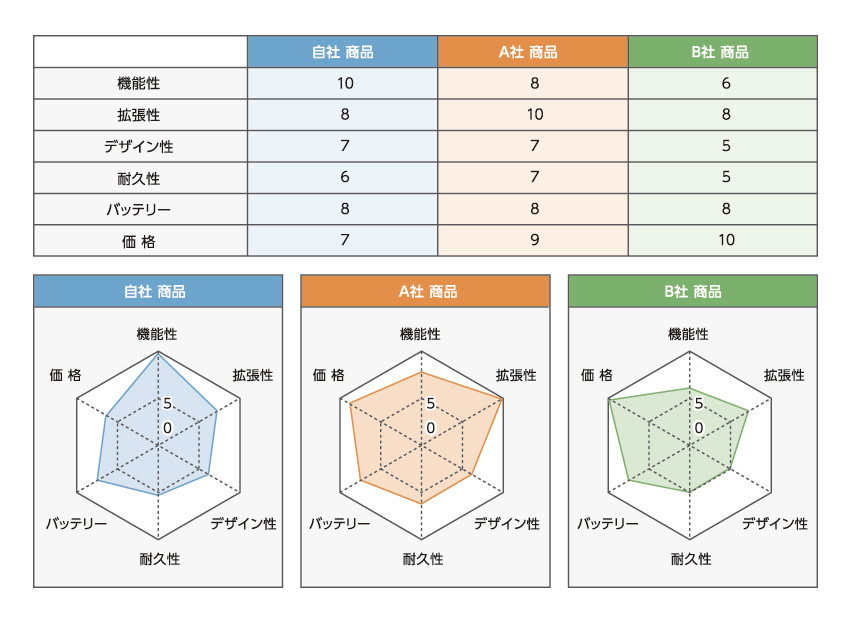
「レーダーチャート」の例 (商品スペックの比較)
 比較しやすくするポイント
比較しやすくするポイント
・属性の似ている項目同士を隣同士に置く
・図形内部を塗りつぶす、メモリの数値を書き込むなど、見やすく工夫する
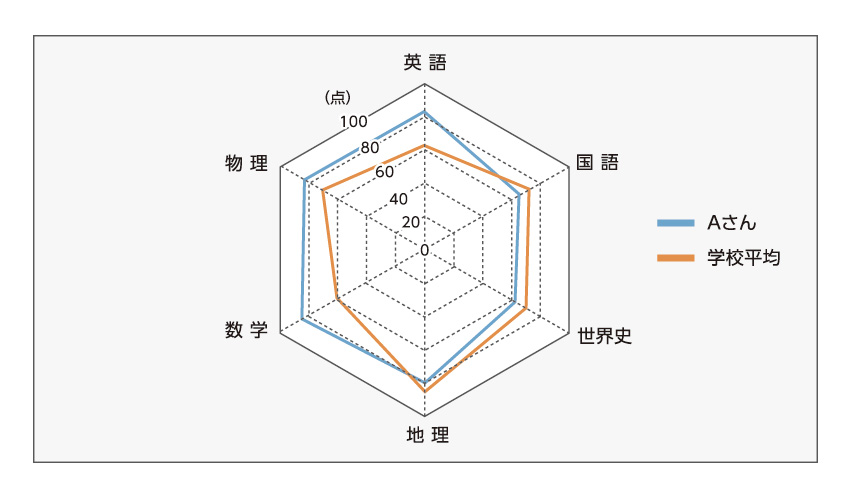
「レーダーチャート」の例 (実力テストにおける学校とAさんの比較)
 比較しやすくするポイント
比較しやすくするポイント
・各項目の平均値を求めて図形内に表示する
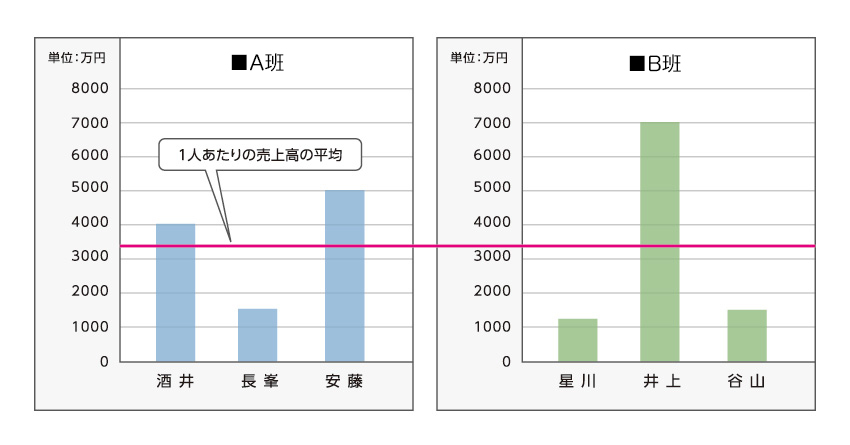
レーダーチャートは放射状の軸と、クモが巣を張ったような軸からなり、「クモの巣」や「スターチャート」とも呼ばれます。ひと目で各項目のバランスが把握できるのが特徴で、製品やサービスの性能比較などに便利です。見やすさを考えると、五角形から八角形くらいになるよう項目数を設定するのが良いでしょう。
「バブルチャート」の例(受注件数、売上高、売上シェアの比較)
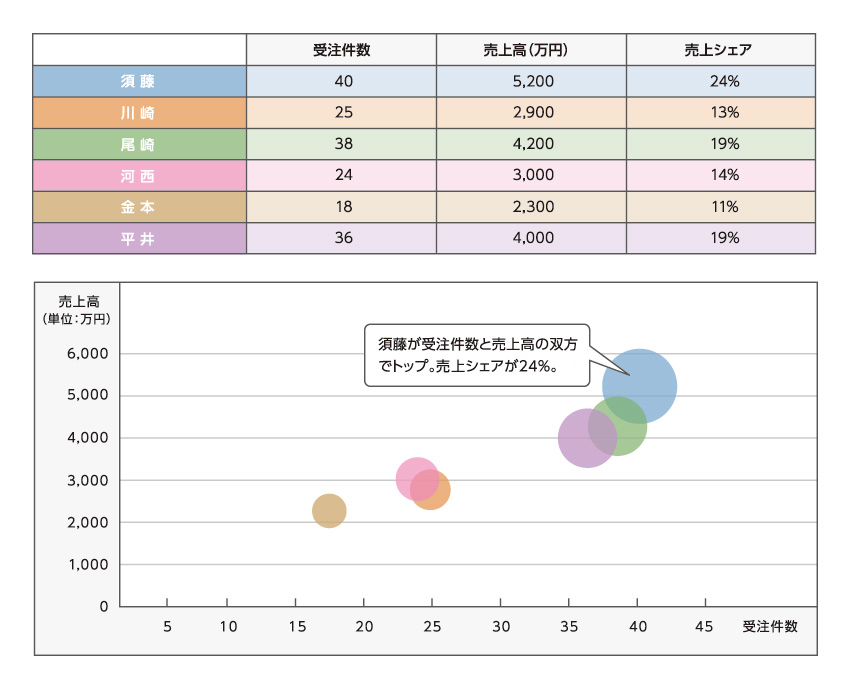 比較しやすくするポイント
比較しやすくするポイント
・バブルの重なり方を考えてメモリの間隔を設定する
・バブルの重なっている部分の色を濃くする
バブルチャートの特徴は、縦軸と横軸に加えて、3番目の値である項目の大きさをバブル(円)の大きさで表現できることです。例えば縦軸に受注件数、横軸に売上高、売上シェアをバブルの大きさで示して、事業を3軸から分析することができます。ほかにも、顧客満足度などを把握するためのポートフォリオ分析など、応用の幅が広いため、重要なビジネスシーンにもしばしば登場します。
「ボリュームチャート」の例(商品スペックの比較)
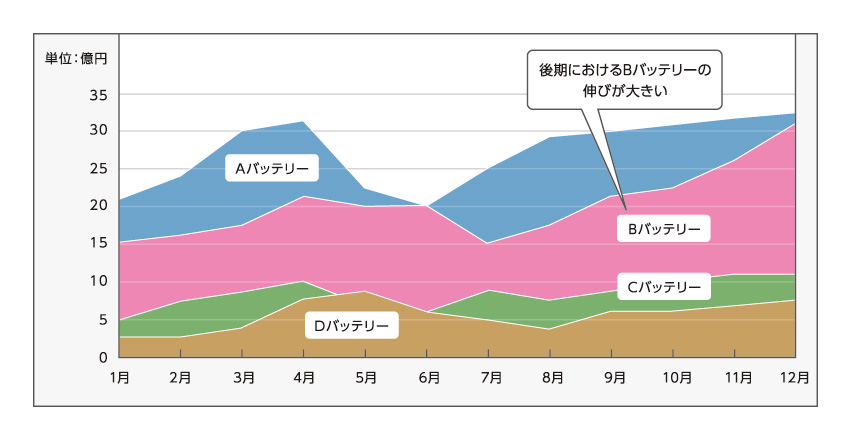 比較しやすくするポイント
比較しやすくするポイント
・強調したい項目の色を濃くするなどカラーリングで工夫
・各項目の名前をラベルとして図中に配置する
・データから分析した解説を図中にフキダシとして埋め込む
ボリュームチャートでは、各項目の時系列にそった変化量をわかりやすく表すことができます。面の大きさは規模を表しているので、総量や構成比率などを把握しやすいのも特徴。毎月の売上データをボリュームチャート化すれば、ある月に意外な商品が売れているなど、思わぬ動きも発見しやすくなります。